This website is a semi-functional mirror of the original Project Euler. More information is available on GitHub.

Euler's Number
Problem 330
Published on 27 March 2011 at 05:00 am [Server Time]
An infinite sequence of real numbers a(n) is defined for all integers n as follows:
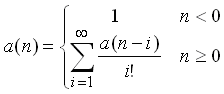
with e = 2.7182818... being Euler's constant.
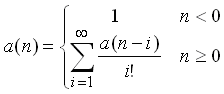
For example,
| a(0) = |
|
+ |
|
+ |
|
+ ... = e − 1 |
| a(1) = |
|
+ |
|
+ |
|
+ ... = 2e − 3 |
| a(2) = |
|
+ |
|
+ |
|
+ ... = |
|
e − 6 |
| It can be shown that a(n) is of the form |
|
for integers A(n) and B(n). |
| For example a(10) = |
|
. |
Find A(109) + B(109) and give your answer mod 77 777 777.
Go to back to Problems